Area estimation plays a crucial role in a number of studies like in the identification of infected cells, estimation of land area and inspection of circuit elements [1]. But of most the time, the subject of these works are either too small (i.e. cells, circuit elements), too large (i.e. land) or too complex (i.e. cells that are not perfect ellipses, land with a rugged border). And physically measuring their dimensions may require too many resources that makes the task nearly impossible.
But but...with the image processing tools that we have now, no object is too small, too big, too many or too complex. An image of our subject and some working knowledge of Green's Theorem is all that we need to have a fairly accurate estimate of an object's area.
Consider a region R whose contour is taken in the counterclockwise direction as shown below. We let F1 and F2 be continuous functions having continuous partial derivatives everywhere in the region R.
Figure 1. Region R
Relating a double integral to a line integral, we get [1]
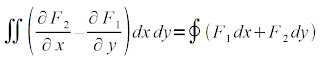
And if we choose F1 = 0, F2 = x, F1 = -y and F2 = 0, the above equation will yield [1]
By averaging the equations above, we get the area A of region R as shown below [1].
If there are Nb pixels in the boundary or contour of region R, then the area A of R is [1]
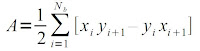
To first test the implementation of the Green's Theorem, I used the code in Activity 2 to generate basic images with analytically known areas. Since the images I'm using is binarized, another way of computing for the area of my target object is by getting the sum of the pixels in my region R by using the sum(im) function where im is my binarized image. I then compare the accuracies of the areas computed using the Green's Theorem technique and the summing technique with my analytic result. From BA, I got the idea of also exploring the accuracies of these methods as the image dimensions are scaled. These I do for two images, that of a centered circle and a square aperture. The code I've for this part of the activity is shown below.
Assigning new values to a variable does not really clear the variable of its previous contents. When I run the program using a different image but the same variable names, I encounter this error
To address this, I first clear the contents of my variables at the start of my program before using them as shown below.

The circle images I used and the areas I got using the analytic, summing and Green's Theorem methods together with the accuracies of the two computational methods are shown below.

Figure 2. Circle Images with Radius from 0.5 in to 3 in
Table 1. Area of a Circle with Different Radius
The square images I used and their corresponding areas gotten using the process outlined above is as follows.
The summary of the results of the summing and Green's theorem methods for the circle and square images of varying dimensions are shown below.
[2] A. Taylor, "Disaster unfolds slowly in the Gulf of Mexico", The Big Picture, retrieved June 29, 2010 from http://www.boston.com/bigpicture/2010/05/disaster_unfolds_slowly_in_the.html.
[3] "Timeline: Gulf of Mexico oil spill", ABS-CBN news.com, retrieved June 29, 2010 from http://www.abs-cbnnews.com/global-filipino/world/06/01/10/timeline-gulf-mexico-oil-spill.
The summary of the results of the summing and Green's theorem methods for the circle and square images of varying dimensions are shown below.
Figure 4. Scaling of Area Estimation
In computing for the area of an object in an image using Green's Theorem, the border or the pixels in the contour are not included in the calculations. Hence, the observed deviation from the analytic area of the target object. This deviation from the theoretical value of the area decreases exponentially as we increase the dimensions of the object as a result of the increase in the surface-to-perimeter ratio. We also see that if the radius of the circle or if half the length of the square is less than 1.00, the computed percent difference for the area of a circle or a square is approximately the same. But as we increase these dimensions, the deviation of the computed area for a square becomes less than that of a circle. We may attribute this to the fact that for a given circle diameter or square length, the perimeter of a circle is greater than a square's perimeter.
When using the sum() function to compute for the area, we get a 100% accuracy for a square. For a circle, on the other hand, we get an almost constant error of 0.20% +/- 0.01%. If we look at the edge of the circle image as shown below, we see that the border is rugged and not smooth. Since every pixel counts in this method, the rugged edge results to the observed error.
Googlemap offers mapping resouces in response to the Gulf of Mexico oil spill crisis. The observed area covered by the oil spill in the gulf is provided by NOAA-NESDIS and can be downloaded from the Google Crisis Response site. An animation of the spread of the oil spill over the gulf for the period May 01 - May 06 is shown below.
There is an observable discrepancy between the areas measured by the summing method and Green's Theorem method. Aside from the earlier stated effect of the exclusion of the border in the Green's Theorem method, there were also some pixels that are not connected to the biggest component and these were also excluded by the follow() function in its tracing of the edge. In cases like this when the areas are too complex, the summing function is more reliable.
Nonetheless, the trends in the spreading of the oil spill in both methods are similar. A decrease in the area covered by the spill is observed on May 4. We can attribute this to the fact that Obama visited the site on May 03 and BP subsequently issued a statement of May 4 stating that cleanup operations were working [3]. Around May 05 - May 06, the weather pattern was reported to be bringing winds of high velocities and as seen above, this may have caused the further spreading of the oil spill [3].
With a little modification of the code, we may further trace the spread of the oil spill to later dates. Knowing how the spill is behaving in response to weather patterns and cleanup operations can help make efforts of saving the gulf more efficient.
Since I gave a thorough explanation of the ways of how we can estimate areas and discussed some of their limitaions, I give myself 10/10.
[1] M. Soriano, "A4-Area Estimation for Images with Defined Edges", AP 186 Handout (June 2010).When using the sum() function to compute for the area, we get a 100% accuracy for a square. For a circle, on the other hand, we get an almost constant error of 0.20% +/- 0.01%. If we look at the edge of the circle image as shown below, we see that the border is rugged and not smooth. Since every pixel counts in this method, the rugged edge results to the observed error.
It is also seen that as the dimensions are increased, not only do the accuracies of the areas computed using the Green's Theorem and the summing method increases but the two methods also approach approximately the same level of accuracy. In general however, the summing method still performs better than the Green's theorem method. Using these methods we have established, we can now compute for areas of more complex shapes with no known analytic solution.
Area estimation can play a crucial role not only in researches performed inside the laboratory but it can also be useful in efforts to hamper potentially harmful effects of an "unprecedented environmental disaster" [2]. Last April 20, a blast on the Deepwater Horizon drilling rig licensed to the BP oil company at the Gulf of Mexico triggered millions of liters of oil to spill over 100 miles of coastline [3].
Figure 6. Gulf of Mexico Oil Spill.
Images taken from http://www.boston.com/bigpicture/2010/05/disaster_unfolds_slowly_in_the.html.
Figure 7. Gulf of Mexico Ecosystem Endangered by the Spill.
Images taken from http://www.boston.com/bigpicture/2010/05/disaster_unfolds_slowly_in_the.html.
The extent of the damage continues to endanger the ecosystem of the Gulf of Mexico [3]. Other oil companies and the US government have joined BP in their attempts to mitigate the spreading of the leak. Containment booms are being erected, protective barriers are being built and devices are being lowered to cap the leaks [2]. To assess the extent to which these efforts are working, tracking the spread and the area covered by the spill is one of the tasks continuously undertaken by experts involved in the control and containment of this disaster [2]. Automating the task of observing the spread of the spill will give the experts more time to actually work on the oil spill cleanup drive. It is here where we can utilize the techniques we've explored earlier concerning area estimation.
Googlemap offers mapping resouces in response to the Gulf of Mexico oil spill crisis. The observed area covered by the oil spill in the gulf is provided by NOAA-NESDIS and can be downloaded from the Google Crisis Response site. An animation of the spread of the oil spill over the gulf for the period May 01 - May 06 is shown below.
Images taken from http://www.google.com/crisisresponse/oilspill/.
The oil spill is shown in green. Using the impixel() function in Matlab, I saved the value of a pixel in the oil spill region in the image. I then scanned the whole image and binarized it such that only areas having pixel values equal to that I saved will be shown in white. The result of this binarization is shown below.
Using the follow() function in Scilab, I then traced the contour for the coordinates of the border. This is necessary for the application of the Green's Theorem method in the estimation of the area.
Figure 10. Edge of Observed Oil Spill in the Gulf of Mexico. (Click to view animation)
I used the two methods developed earlier, the summing method and the Green's Theorem method for the estimation of the area covered by the oil spill. The results of which are shown below.
Table 3. Observed Oil Spill in the Gulf of Mexico
Figure 11. Observed Oil Spill in the Gulf of Mexico
There is an observable discrepancy between the areas measured by the summing method and Green's Theorem method. Aside from the earlier stated effect of the exclusion of the border in the Green's Theorem method, there were also some pixels that are not connected to the biggest component and these were also excluded by the follow() function in its tracing of the edge. In cases like this when the areas are too complex, the summing function is more reliable.
Nonetheless, the trends in the spreading of the oil spill in both methods are similar. A decrease in the area covered by the spill is observed on May 4. We can attribute this to the fact that Obama visited the site on May 03 and BP subsequently issued a statement of May 4 stating that cleanup operations were working [3]. Around May 05 - May 06, the weather pattern was reported to be bringing winds of high velocities and as seen above, this may have caused the further spreading of the oil spill [3].
With a little modification of the code, we may further trace the spread of the oil spill to later dates. Knowing how the spill is behaving in response to weather patterns and cleanup operations can help make efforts of saving the gulf more efficient.
Since I gave a thorough explanation of the ways of how we can estimate areas and discussed some of their limitaions, I give myself 10/10.
[2] A. Taylor, "Disaster unfolds slowly in the Gulf of Mexico", The Big Picture, retrieved June 29, 2010 from http://www.boston.com/bigpicture/2010/05/disaster_unfolds_slowly_in_the.html.
[3] "Timeline: Gulf of Mexico oil spill", ABS-CBN news.com, retrieved June 29, 2010 from http://www.abs-cbnnews.com/global-filipino/world/06/01/10/timeline-gulf-mexico-oil-spill.

















No comments:
Post a Comment